Summary/Abstract

Mechanism analysis or kinematics of machines is inherently a vital part in machine design.   Inversion is the process of fixing different links in a chain to create different mechanism.  Many useful mechanisms may be obtained by the inversion of various kinematics chains.  An example of such inversion can be seen in Crank and Slotted Quick return motion.  In this experiment, the relative motion of the kinematic pairs is sliding which related to the movement of the slotted lever.  This principle of action is the same that applied to the reciprocating engine. 

The objective is to investigate the kinematic motion of a Crank and Slotted Lever Quick Return Motion mechanism and to verify that the motion does have quick return stroke and a slow cutting or forward stroke.  Then, the investigation is to show that it will increase the efficiency if applied to a machine tool. The apparatus used is shown in the Appendix.  The result is obtained by rotating the crank by 10° increments and the corresponding slider position is taken.  This step is repeated for a full 360° rotation.  The result of the experiment is tabulated in Table 1 shown at the Data, Observation and Calculation of Results section.  The graph of both experimental and theoretical slider position, x against the crank angle is plotted in one graph (FIGURE 1) and the return and cutting strokes range were shown.  From the experiment, the recorded results of the slider position together with the crank angle will contribute to a sinusoidal graph.  Noted that initially, the slider position is at 70mm for crank angle of zero and 180 degrees.  With reference to FIGURE 1, the theoretical and measured values of the slider position shows a small deviation since error is generated during experiment.  The average error is about 2.1%.  The error may be due to the parallax error had occur when the readings is taken.  The return stroke occupies 160°, which are about 44.44 % from one full revolution.  The cutting stroke occupies 200°, which are about 55.56% from one full revolution.  It can clearly be seen that the value of the return stroke rotation angle is smaller compared to the cutting stroke rotation angle due to the quick return motion.  The increase in efficiency is 11.12 %.

The table below shows the maximum and minimum value of the slider position theoretically and experimentally.

In conclusion, the experiment is successfully done since the experimental results tend to agree to the theoretical aspects of the experiment.  It has been proven and verified that the Crank and Slotted Lever mechanism does have a quick return stroke and a slow cutting or forward stroke with an increase in efficiency of the machine tool.

Objectives

The main purpose of this experiment is to investigate the kinematic motion of a Crank and Slotted Lever Quick Return Mechanism.  The investigation is to show that it is indeed a quick return mechanism and then the evaluation of the increase in efficiency that the system may offer if it is applies to a machine tool will be done.

Apparatus

Crank and Slotted Lever Quick Return Mechanism

Procedures

1.      The crank is set to zero so that the pointer at the scale begins at the initial position.

2.      The position of the crosshead, x is recorded.

3.      The crank is rotated by 10° increment and again the x value will be recorded in the table. 

4.      Steps above were repeated until one complete revolution of the crank.

Data, Observation and Calculation of Results

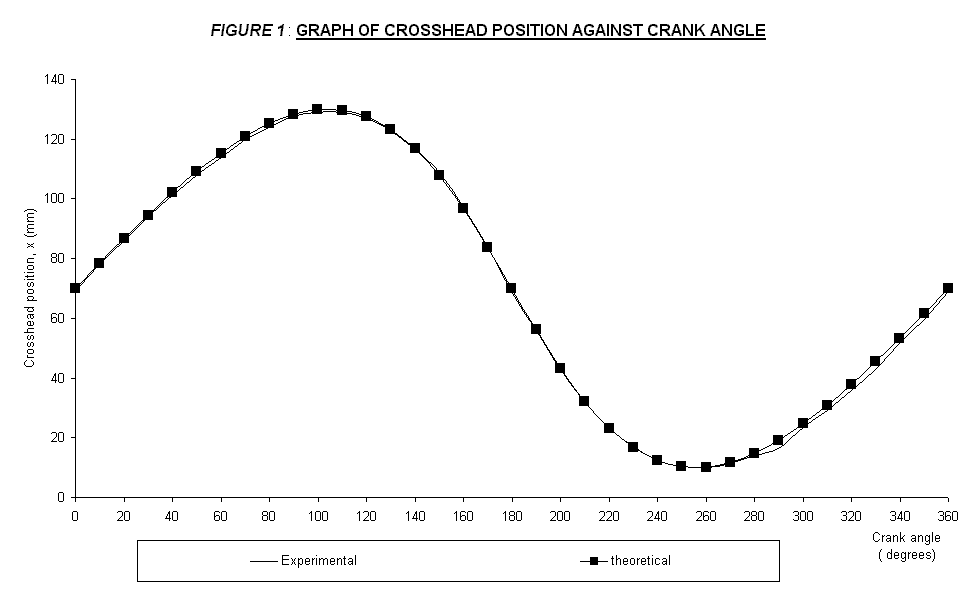
Table 1 below shows the experimental and theoretical results.  From the data recorded, the graph of measured and theoretical crosshead position against crank angle was plotted in FIGURE 1, attached in the Appendix.  From the plotted graph, the return and cutting strokes range was shown.  The calculation of the theoretical values is shown in the Appendix.

Table 1

Discussion

            From the experimental data tabulated in Table 1 and the plotted graph, the maximum experimental slider position, x is 129 mm, occurs between 100° and 110°.    The minimum slider position, at 10 mm, occurs at 260°.  With reference to the plotted graph, by considering the minimum and maximum slider position point and assuming that the mechanism is rotating at a constant speed, it can be said that the return stroke occupies about 160° (from 100° to 260°), which is about 44.44% from the full revolution.   The cutting stroke occupies about 200° (from 0° to 100° and again from 260° to 360°), which is about 55.56% from the full revolution. So, it can be said that the return stroke takes less percentage of crank revolution compared to the cutting stroke. Thus, the return stroke requires less energy to operate and less time taken compared to the cutting stroke.

The possible maximum increase in efficiency is calculated.  It is about 11.12%.  With reference to FIGURE 1, it can be said that the shape of the experimental results has the same shape to the theory of this experiment, which are slow cutting stroke and a fast return stroke.  Therefore, the experimental result tends to agree to the predictions from the theory of the experiment.  The graph shows that the slope in the return stroke region is steeper than the slope in the forward cutting stroke.  The cutting stroke takes higher percentage crank revolution so it can be assume that it requires more power and work to operate it compared to the return stroke due to the mechanism of the quick return motion. 

The result of the experiment shows a small deviation compared to the theoretical value with an average percentage error for about 2.1 %. The difference between the theoretical and the experimental results may caused by parallax error occur when the readings was taken and also during setting the pointer at the specific angle, where the pointer is not accurately set to the intended angle.  All the calculation involving the theoretical and error values were shown at the Appendix section.  Although error exist, but it does not effect in terms of confirming that the crank and slotted lever has a quick return mechanism that may increase the efficiency if it is applied to a machine tool.

Table 2 below shows the percentage error value at each crank angle.

Table 2

Average percentage error = 2.1 %

Conclusion

In conclusion, with the aid of the ‘crank and slotted lever quick return mechanism’ apparatus, the kinematic motion of a Crank and Slotted Lever Quick Return mechanism has been investigated.  It is proven that this quick return motion mechanism will definitely increase the efficiency of the machine tool because the return stroke takes less percentage of crank angles compared with the cutting stroke. Therefore, the occurrence of the cutting stroke can be done in many instances. The increase in efficiency shows that the advantages of the mechanism.  This mechanism, often used in equipment such as machine tools and production machinery can be used to produce long, slow movements for forward or cutting stroke and faster return stroke in which less energy is consumes for a constant angular velocity of the driving crank.

Reference

Mechanical design and CAD laboratory (MEMB 321) lab manual

Appendix

A.     Inversion of the slider-crank chain

                   C                                      240 mm

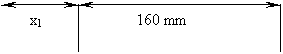
FIGURE 2: Known dimensions of the crank and quick return mechanism

               Initially, the slider position is at 70mm when the crank angle, q is zero and 180 degrees.  The known values are the crank radius, OB is 40mm.   The slotted lever length, AC is 240mm and the distance OA is 160mm. 

v     In order to determine the theoretical values of the slider position, basic trigonometry must be applied.  The governing theoretical equation is shown below.

Y = 40 sin q

X₁ = 40 cos q

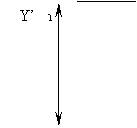
Y’ = 240 sin a

In order to find Y’, a must be determine first.

From trigonometry, a = tan^-1  (       Y          )

                                                    160 + X₁

\ Theoretical slider position, X = 70 + Y’

v     Percentage of the crank revolution occupied by each stroke

 = angle occupied * 100

                                                            360

v     Increase in efficiency, h

= % of crank revolution in cutting stroke - % of crank revolution in return stroke

v     Percentage error = (x theoretical – x experimental )  * 100

x experimental

B.      Sample calculation in determining the slider position with crank angle of 10°

v     Theoretical slider position:

Y = 40 sin q = 40 sin 10° = 6.9459

X₁ = 40 cos q = 40 cos 10° = 39.3923

Y’ = 240 sin a

In order to find Y’, a must be determine first.

From trigonometry, a = tan^-1  (       Y       ) = tan^–1 [6.9459 / (160+39.3923)] = 1.9951°

                                                    160 + X₁

\ Y’ = 240 sin a = 240 sin 1.9951° = 8.3354 mm

\ Theoretical slider position, X = 70 + Y’ = 70+8.3354 = 78.3554 =78.36 mm

v     Percentage of the crank revolution occupied by each stroke

 = angle occupied * 100

                                                            360

- Rotation angle for cutting stroke = 200 degrees

- Rotation angle for return stroke = 160 degrees

            \For cutting stroke:  (200 / 360) x 100 = 55.56 % from one full revolution

            \For return stroke:  (160 / 360) x 100 = 44.44 % from one full revolution

v     Increase in efficiency, h

= % of crank revolution in cutting stroke - % of crank revolution in return stroke

 Therefore, the efficiency is given by:

                        Efficiency, h = 55.56 % - 44.44 % = 11.12 %

v     Percentage error = (x theoretical – x experimental )  * 100

x theoretical

= (78.36 – 70) *100 = 0.5 %

                                            78.36  

v     Average percentage error = sum of all % error = 2.1%

          37