Summary/Abstract

A universal joint is used where the angularity between the shafts is intentional. A Hooke’s Coupling is a fixed arm coupling. This experiment is concerning to the study of a Hooke’s Coupling which transmit rotation from one axis to another using the Hooke’s coupling apparatus, shown in the Appendix. Indeed continuous circular motion is perhaps the single largest thing that mankind produces in the world with available energy.

The objective and purpose of this experiment is to investigate the variation in displacement for a single joint at various angles and to show that when two joints are used together with the same intermediate angle, the variation in displacement is cancelled out. There are two parts in the experiment. In Part 1, various values of a₁ (angle of the driving shaft) are used that is 15, 30 and 45 degrees, while the driving shaft angle, a₂is set to 0°. For Part 2, both value of a is being fixed at 30° but in different orientation, that is bent and parallel conditions. In order to achieve the objective of this experiment, several reading were taken with the increments of 10° of the input shaft.

Theoretically, the angle between the shafts is proportional to the speed and torque, where the increase of the angle will offer a periodic speed and hence torque fluctuation. Such fluctuation cannot be tolerated in machinery so it is usual to have two couplings with a small intermediate shaft. Below are the findings of the experiment:

1. The recorded results of the output shaft angle against the input shaft angle will contribute to an almost a linear graph. By observing carefully, there is a fluctuations for different value of alpha, a, where the larger the value of alpha, a, the bigger the deflection is.

2. From the graph of the output shaft velocity against the input shaft angle, the plot shows that the larger the angle, the speed become periodic with bigger amplitude.

3. Theoretically, the graph of tan for input shaft angle versus tan for output shaft angle would appear as linear within the range of 0° to 80°. On the other hand, the plotted graph produced almost a linear plot. So, the plot is enough to reveal that tan q is directly proportional to tan f. This proves that the theory statement:

· tan f = tan q cos a

4. In Part 2, the values obtained for the output shaft in bent or parallel condition should be the same in order to cancel out the variation in displacement. Again, the values obtained are not the same that may due to accompanied error.

Finally, the experiment is successfully done since the experimental results tend to agree to the theoretical aspects of the experiment. It has been shown that when two joints are used together with the same intermediate angle, the variation in displacement is cancelled out. Therefore, the apparatus having two couplings with a small intermediate shaft, the fluctuations of the output shaft could be reduced especially in machinery provided that the intermediate angles is the same.

Purpose / Objective

The objective of the experiment is to investigate the variation in displacement for a single joint at various angles and to show that when two joints are used together with the same intermediate angle, the variation in displacement is cancelled out.

Apparatus

Hooke’s Coupling Apparatus

Procedure

· Part 1

1. The left-hand bracket is set over so that the angle, a₁ between the shafts is 45°.

2. The other joint is set to be straight, that is a₂ = 0°.

3. Start with the scale on the input shaft at zero. The shaft is rotated by 10°.

4. The reading on the scales on the input and output shafts was taken and recorded in the table.

5. Steps above were repeated for one complete rotation of the input shaft.

6. Repeat procedures 1 to 5 for a₁ = 15° and 30°.

· Part 2

1. Both angles a₁ and a₂ were set at 30°, bent at the same side.

2. For one revolution of the input shaft (at 10° intervals), the readings of the output shaft scale was taken and recorded in the table.

3. The experiment was repeated with parallel input and output shafts, but the angle is kept at 30°.

Theory

Data, Observation and Calculations of Results

The following are the results of the experiment. From the data recorded, three graphs were plotted, attached in the Appendix. The calculations of the Output velocity values are shown in the Appendix.

· Part 1

Ø For a₁ = 15°

Input, q°	tan q°	Output, f°	tan f°	Output velocity
0	0	3	0.052408	1.03528
10	0.17633	6.5	0.113936	1.03304
20	0.364	17	0.305731	1.02665
30	0.57735	27	0.509525	1.01702
40	0.8391	37	0.753554	1.00545
50	1.19175	47	1.072369	0.99342
60	1.73205	56.5	1.510835	0.98238
70	2.74748	65	2.144507	0.97355
80	5.67128	77	4.331476	0.96788
90	-	85	11.43005	0.96593
100	-5.67128	95	-11.4301	0.96788
110	-2.74748	105	-3.73205	0.97355
120	-1.73205	114	-2.24604	0.98238
130	-1.19175	124	-1.48256	0.99342
140	-0.8391	134.5	-1.01761	1.00545
150	-0.57735	144	-0.72654	1.01702
160	-0.364	155	-0.46631	1.02665
170	-0.17633	165.5	-0.25862	1.03304
180	0	176	-0.06993	1.03528
190	0.17633	186	0.105104	1.03304
200	0.364	197	0.305731	1.02665
210	0.57735	207	0.509525	1.01702
220	0.8391	217	0.753554	1.00545
230	1.19175	227	1.072369	0.99342
240	1.73205	237	1.539865	0.98238
250	2.74748	247	2.355852	0.97355
260	5.67128	257	4.331476	0.96788
270	-	267	19.08114	0.96593
280	-5.67128	275	-11.4301	0.96788
290	-2.74748	285	-3.73205	0.97355
300	-1.73205	294	-2.24604	0.98238
310	-1.19175	304	-1.48256	0.99342
320	-0.8391	314	-1.03553	1.00545
330	-0.57735	324	-0.72654	1.01702
340	-0.364	335	-0.46631	1.02665
350	-0.17633	345	-0.26795	1.03304
360	0	356	-0.06993	1.03528

Table 1

Ø For a₁ = 30°

Input, q°	tan q°	Output, f°	tan f°	Output velocity
0	0	2	0.034921	1.15470
10	0.17633	15	0.267949	1.14321
20	0.364	28	0.531709	1.11137
30	0.57735	38.5	0.795436	1.06588
40	0.8391	49	1.150368	1.01492
50	1.19175	59	1.664279	0.96579
60	1.73205	69.5	2.674621	0.92376
70	2.74748	76	4.010781	0.89211
80	5.67128	85	11.43005	0.87260
90	-	93.5	-16.3499	0.86603
100	-5.67128	101.5	-4.91516	0.87260
110	-2.74748	111.5	-2.53865	0.89211
120	-1.73205	120	-1.73205	0.92376
130	-1.19175	129.5	-1.2131	0.96579
140	-0.8391	140	-0.8391	1.01492
150	-0.57735	150	-0.57735	1.06588
160	-0.364	161	-0.34433	1.11137
170	-0.17633	172	-0.14054	1.14321
180	0	183.5	0.061163	1.15470
190	0.17633	195.5	0.277325	1.14321
200	0.364	207.5	0.520567	1.11137
210	0.57735	219	0.809784	1.06588
220	0.8391	230	1.191754	1.01492
230	1.19175	239	1.664279	0.96579
240	1.73205	248.5	2.538648	0.92376
250	2.74748	257	4.331476	0.89211
260	5.67128	265.5	12.7062	0.87260
270	-	273.5	-16.3499	0.86603
280	-5.67128	282.5	-4.51071	0.87260
290	-2.74748	292	-2.47509	0.89211
300	-1.73205	301.5	-1.63185	0.92376
310	-1.19175	311.5	-1.13029	0.96579
320	-0.8391	320.5	-0.82434	1.01492
330	-0.57735	330.5	-0.56577	1.06588
340	-0.364	341	-0.34433	1.11137
350	-0.17633	352	-0.14054	1.14321
360	0	363	0.052408	1.15470

Table 2

Ø For a₁ = 45°

Input, q°	tan q°	Output, f°	tan f°	Output velocity
0	0	1	0.017455	1.41421
10	0.17633	12	0.212557	1.37282
20	0.364	24.5	0.455726	1.26611
30	0.57735	36	0.726543	1.13137
40	0.8391	46	1.03553	1.00073
50	1.19175	56	1.482561	0.89122
60	1.73205	64	2.050304	0.80812
70	2.74748	72	3.077684	0.75103
80	5.67128	79	5.144554	0.71793
90	-	86.5	16.34986	0.70711
100	-5.67128	93	-19.0811	0.71793
110	-2.74748	100	-5.67128	0.75103
120	-1.73205	112	-2.47509	0.80812
130	-1.19175	115	-2.14451	0.89122
140	-0.8391	125	-1.42815	1.00073
150	-0.57735	135	-1	1.13137
160	-0.364	147	-0.64941	1.26611
170	-0.17633	163	-0.30573	1.37282
180	0	176	-0.06993	1.41421
190	0.17633	191	0.19438	1.37282
200	0.364	205	0.466308	1.26611
210	0.57735	215	0.700208	1.13137
220	0.8391	225	1	1.00073
230	1.19175	235.5	1.455009	0.89122
240	1.73205	243	1.962611	0.80812
250	2.74748	252	3.077684	0.75103
260	5.67128	259.5	5.395517	0.71793
270	-	267	19.08114	0.70711
280	-5.67128	274	-14.3007	0.71793
290	-2.74748	280	-5.67128	0.75103
300	-1.73205	288	-3.07768	0.80812
310	-1.19175	296	-2.0503	0.89122
320	-0.8391	305	-1.42815	1.00073
330	-0.57735	316	-0.96569	1.13137
340	-0.364	328	-0.62487	1.26611
350	-0.17633	342	-0.32492	1.37282
360	0	358	-0.03492	1.41421

Table 3

· Part 2

Ø For a₁ = a₂ = 30° (shafts are bent at the same side)

Input, q°	Output, f°
0	4
10	14
20	19
30	34
40	45
50	55
60	65
70	75
80	84.5
90	94
100	103.5
110	114
120	124
130	134
140	143.5
150	153
160	163
170	173
180	183
190	193.5
200	205
210	215
220	225
230	235
240	245.5
250	255
260	264
270	274
280	284
290	294.5
300	305
310	315
320	324
330	333
340	343
350	353
360	363

Table 4

Ø For a₁ = a₂ = 30° (shafts are parallel to each other)

Input, q°	Output, f°
0	3.5
10	13
20	24
30	34
40	44
50	54
60	64
70	73.5
80	84
90	93.5
100	104.5
110	115
120	126
130	135
140	145.5
150	155.5
160	163.5
170	173.5
180	182
190	192
200	203
210	213
220	223
230	233
240	243
250	254
260	263
270	273
280	283
290	296
300	304
310	316.5
320	327
330	336
340	344.5
350	354.5
360	363.5

Table 5

Discussion

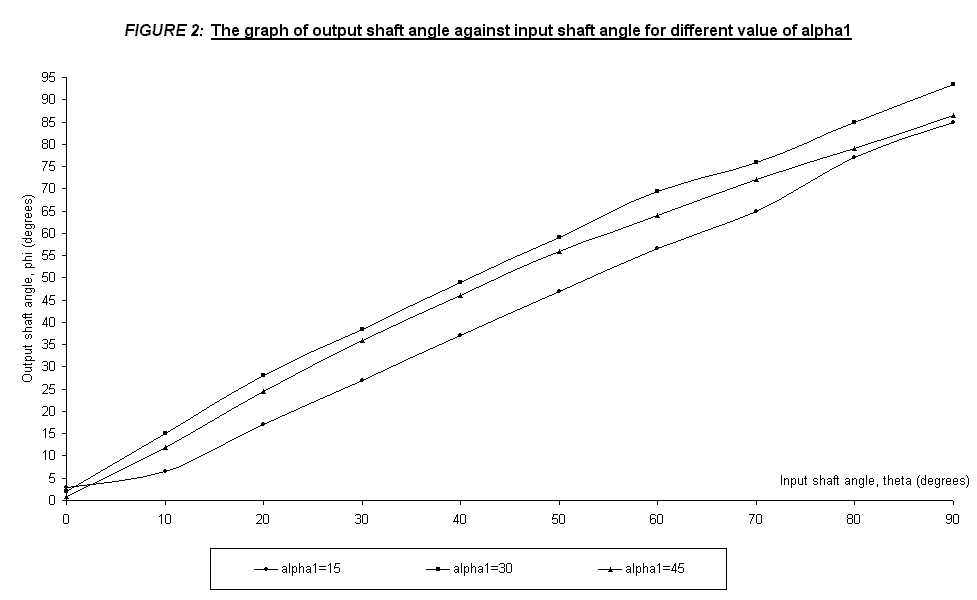
The graph of Output shaft angle against Input shaft angle (FIGURE 1 and FIGURE 2) shows that the variation in displacement is about the same for a₁ set to 15°, 30° and 45°. The plot of the output shaft angle against the input shaft angle tends to agree with the theoretical statement where such arrangement of the fixed arm coupling will produced periodic speed and hence torque deflection whenever the shaft angle, a is being increased. The fluctuation is directly proportional to the angle between shaft. The fluctuation can be seen clearly if larger value of shaft angle is applied and vice versa. Also note that the displacement pattern is an inversion from one range to another that is displacement for 90° to 180° is the inversion of the plot pattern from 0° to 90°.

From the graph of tan for input shaft angle against tan for output shaft angle (FIGURE 3), the plots were not linear as the theoretical plot. But, the plot is enough to reveal that tan q is directly proportional to tan f. This proves that the theory statement:

· tan f = tan q cos a

It is proved that the larger the angle, the less steep the graph is. In order to avoiding complexity, the plot is within the range of 0° to 80° only. The value for tan 90° is neglected in the plotting because the value at infinity cannot be exactly computed. The plots did show the validity in investigating the variation of displacement in the laboratory although there exist some error that cause the plots not very perfect in shape but it is sufficient to agree and to approved the theoretical point of view.

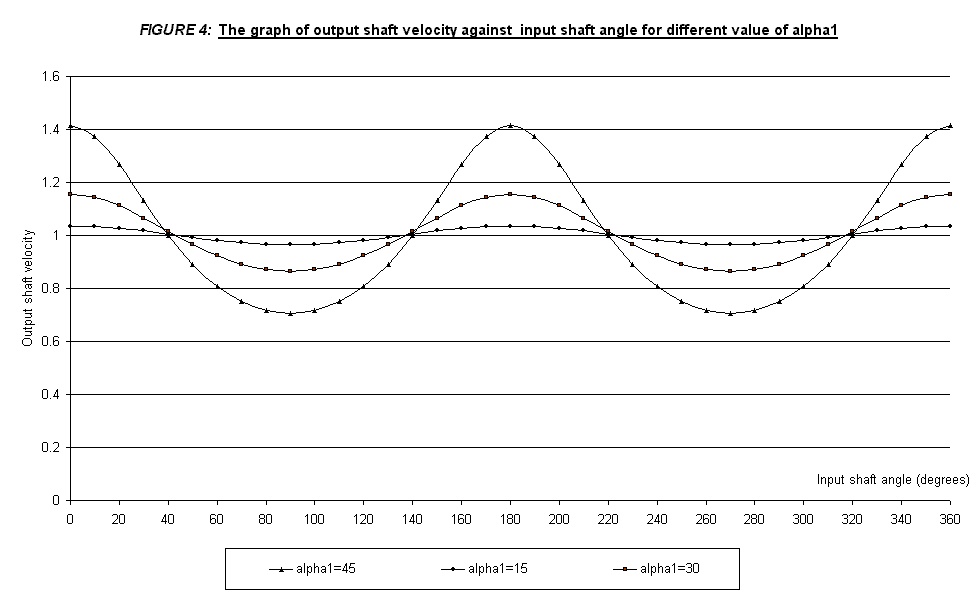
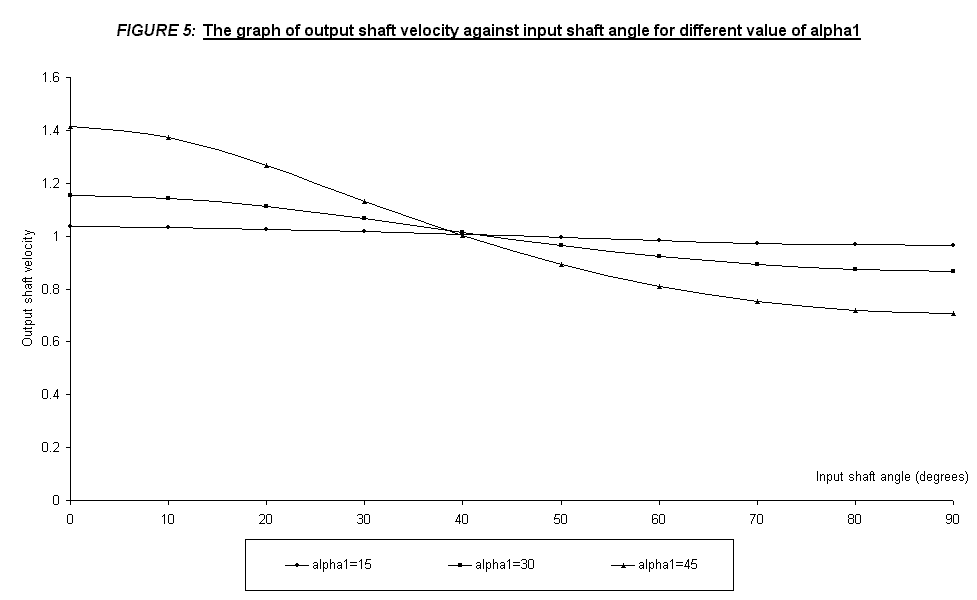
The output shaft velocity plotted in FIGURE 4 and FIGURE 5 shows that the velocity variations that were obtained experimentally does agreed with the theoretical explanation that is the Hooke’s Coupling velocity fluctuates. The graphs show a sinusoidal shape. It can be seen from the graph that the larger the value of a, the bigger the amplitude of the deflection is. This is due to the condition where angle between the shafts formed periodic speed and hence torque fluctuations. The reason is when the angle getting larger, the stability of the shafts is decreased while operating and thus, fluctuation may increase.

The purpose of the second part of the experiment (Part 2) is to show that when two joints are used together with the same intermediate angle, the variation in displacement is cancelled out, whether the shafts is in bent or parallel orientation. Theoretically, the values obtained for the angle between the shafts should be the same for input and output shaft angle (in this experiment the value is fixed at 30 degrees) in order to cancel out the displacement. Unfortunately, the values of the output angle that being determined experimentally was not as the same as the input shaft angle that may be due to error such as personal error during taking the readings and during setting the pointer at the specific angle, where the pointer is not accurately set to the intended angle or systematic error that related to the ineffectiveness of the apparatus. The difference is about 4 to 5 degrees. Although, error has occur, the intention to justify the purpose of the experiment is achieved since the difference does not vary greatly. . However, the displacement cancellation could not be achieved completely through experiment due to errors.

The most important is, for the second part of the experiment, the value of the angle between shafts, that is a₁ and a₂ must be fixed at the same angle in order to prove that the displacement can be cancelled out. It can be achieved both for bent and parallel shafts condition. Therefore, if a₁ and a₂ angle is different, the intention to prove the statement in the objective could not be done. In addition, if both angle is not similar, the second part experiment will be the same with the first part of this experiment. As a result, there will be a variation in the displacement since the variation in displacement effects is not cancelled out.